Table Of Content

Another way to look at these residuals is to plot the residuals against the two factors. Notice that pressure is the treatment factor and batch is the block factor. Both the treatments and blocks can be looked at as random effects rather than fixed effects, if the levels were selected at random from a population of possible treatments or blocks. We consider this case later, but it does not change the test for a treatment effect.
Analysis of Variance:Table of Contents
All variance that can't be explained by the independent variable is considered error. By adding the blocking variable, we partition out some of the error variance and attribute it to the blocking variable. As a results, there will be three parts of the variance in randomized block ANOVA, SS intervention, SS block, and SS error, and together they make up SS total. In doing so, the error variance will be reduced since part of the error variance is now explained by the blocking variable.
Assign treatments to blocks
For instance, if you had a plot of land the fertility of this land might change in both directions, North -- South and East -- West due to soil or moisture gradients. As we shall see, Latin squares can be used as much as the RCBD in industrial experimentation as well as other experiments. Second, the blocking variable cannot interact with the independent variable. In the example above, the cell phone use treatment (yes vs. no) cannot interact with driving experience.
4 Outlook: Multiple Block Factors
The row and column and treatment all have the same parameters, the same effects that we had in the single Latin square. In a Latin square, the error is a combination of any interactions that might exist and experimental error. To compare the results from the RCBD, we take a look at the table below. What we did here was use the one-way analysis of variance instead of the two-way to illustrate what might have occurred if we had not blocked, if we had ignored the variation due to the different specimens. We consider an example which is adapted from Venables and Ripley (2002), the original source isYates (1935) (we will see the full data set in Section 7.3). Atsix different locations (factor block), three plots of land were available.Three varieties of oat (factor variety with levels Golden.rain, Marvellousand Victory) were randomized to them, individually per location.
The World Trade Center, by the Numbers HISTORY - History
The World Trade Center, by the Numbers HISTORY.
Posted: Thu, 02 Sep 2021 07:00:00 GMT [source]
Design Systems Adoption Statistics
The only randomization would be choosing which of the three wafers with dosage 1 would go into furnace run 1, and similarly for the wafers with dosages 2, 3 and 4. An ANOVA table provides all the information an experimenter needs to (1) test hypotheses and (2) assess the magnitude of treatment effects. I have a Master of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
The Legendary Small-Block Chevy V-8: A Look Back at Its Highlights and Evolution - MotorTrend
The Legendary Small-Block Chevy V-8: A Look Back at Its Highlights and Evolution.
Posted: Tue, 28 Feb 2023 23:38:29 GMT [source]
This subset of columns from the whole Latin Square creates a BIBD. With our first cow, during the first period, we give it a treatment or diet and we measure the yield. Obviously, you don't have any carryover effects here because it is the first period. However, what if the treatment they were first given was a really bad treatment?
How to Carry Out a Randomized Block Design
My business insights are based on real-world experience, ensuring that aspiring entrepreneurs can confidently start and run their own businesses. 🙂 We tried our best to provide all the Design Systems statistics on this page. Please comment below and share your opinion if we missed any Design Systems statistics. Strictly Necessary Cookie should be enabled at all times so that we can save your preferences for cookie settings. The calculator reports that the probability that F is greater than 4.4 equals about 0.04.
In this case, we would have four rows, one for each of the four varieties of rice. In this case, we have five columns, one for each of the five blocks. In each block, for each treatment, we are going to observe a vector of variables.
Then, under the null hypothesis of no treatment effect, the ratio of the mean square for treatments to the error mean square is an F statistic that is used to test the hypothesis of equal treatment means. In some disciplines, each block is called an experiment (because a copy of the entire experiment is in the block) but in statistics, we call the block to be a replicate. This is a matter of scientific jargon, the design and analysis of the study is an RCBD in both cases.
However, this method of constructing a BIBD using all possible combinations, does not always work as we now demonstrate. If the number of combinations is too large then you need to find a subset - - not always easy to do. However, sometimes you can use Latin Squares to construct a BIBD. As an example, let's take any 3 columns from a 4 × 4 Latin Square design.
It is important to have all sequences represented when doing clinical trials with drugs. Here is a plot of the least squares means for Yield with all of the observations included. Below is the Minitab output which treats both batch and treatment the same and tests the hypothesis of no effect. They have four different dosages they want to try and enough experimental wafers from the same lot to run three wafers at each of the dosages.
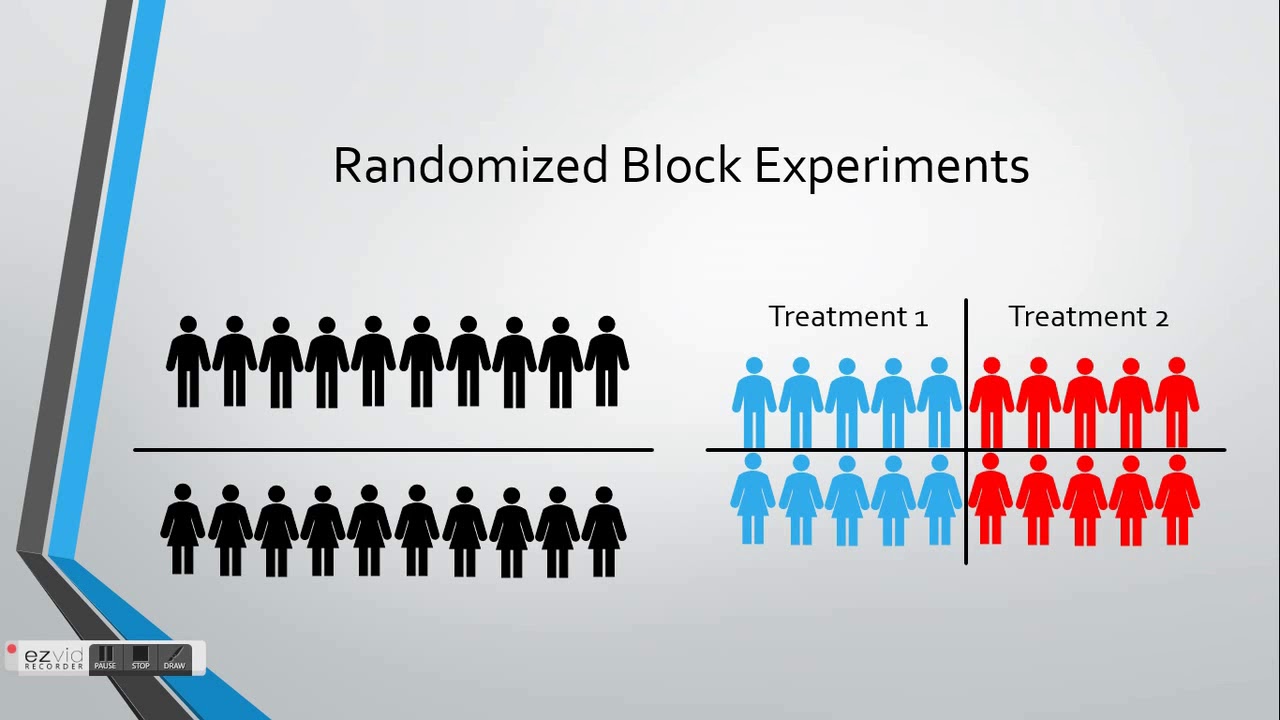
Note that blocking is a special way to design an experiment, or a special“flavor” of randomization. Blocking can also be understood as replicating an experimenton multiple sets, e.g., different locations, of homogeneous experimental units,e.g., plots of land at an individual location. The experimental units shouldbe as similar as possible within the same block, but can be very differentbetween different blocks. This design allows us to fully remove thebetween-block variability, e.g., variability between different locations, fromthe response because it can be explained by the block factor. In that sense, blocking is a so-calledvariance reduction technique.
Each batch of resin is called a “block”, since a batch is a more homogenous set of experimental units on which to test the extrusion pressures. Below is a table which provides percentages of those products that met the specifications. In studies involving human subjects, we often use gender and age classes as the blocking factors. We could simply divide our subjects into age classes, however this does not consider gender. Therefore we partition our subjects by gender and from there into age classes. Thus we have a block of subjects that is defined by the combination of factors, gender and age class.
A completely randomized design (CRD) for the greenhouse experiment is reasonable, provided the positions on the bench are equivalent. In this setting, for example, some micro-environmental variation can be expected due to the glass wall on one end, and the open walkway at the other end of the bench. When we have missing data, it affects the average of the remaining treatments in a row, i.e., when complete data does not exist for each row - this affects the means. When we have complete data the block effect and the column effects both drop out of the analysis since they are orthogonal. With missing data or IBDs that are not orthogonal, even BIBD where orthogonality does not exist, the analysis requires us to use GLM which codes the data like we did previously. We have not randomized these, although you would want to do that, and we do show the third square different from the rest.
We cannot fit a more complex model, includinginteraction effects, here because we do not have the corresponding replicates. Typical block factors are location (see example above), day (if an experiment isrun on multiple days), machine operator (if different operators are needed forthe experiment), subjects, etc. To establish an RCBD for this data, the assignments of fertilizer levels to the experimental units (the potted plants) have to be done within each block separately.

No comments:
Post a Comment